B+Tree History

在实现B+Tree时，遇到了一些模糊概念，所以有了此文，介绍B+Tree出现的来龙去脉。

数据库的核心之一是查询，如何快速找到对应的数据，需要一种适合的数据结构来快速定位。Binary Search Tree就是一种。

Binary Search Trees

二叉搜索树(binary search tree)也称ordered binary tree或sorted binary tree。它是一个Binary Tree，即一个node最多只能有2个children。同时也有称它为m-ary tree，即一个node最多能有m个children，这里m=2。

BST在二叉树的基础上又满足了二分查找算法，即一个node上的key满足：

left sub-tree keys < node key <= right sub-tree keys

如下BST的example

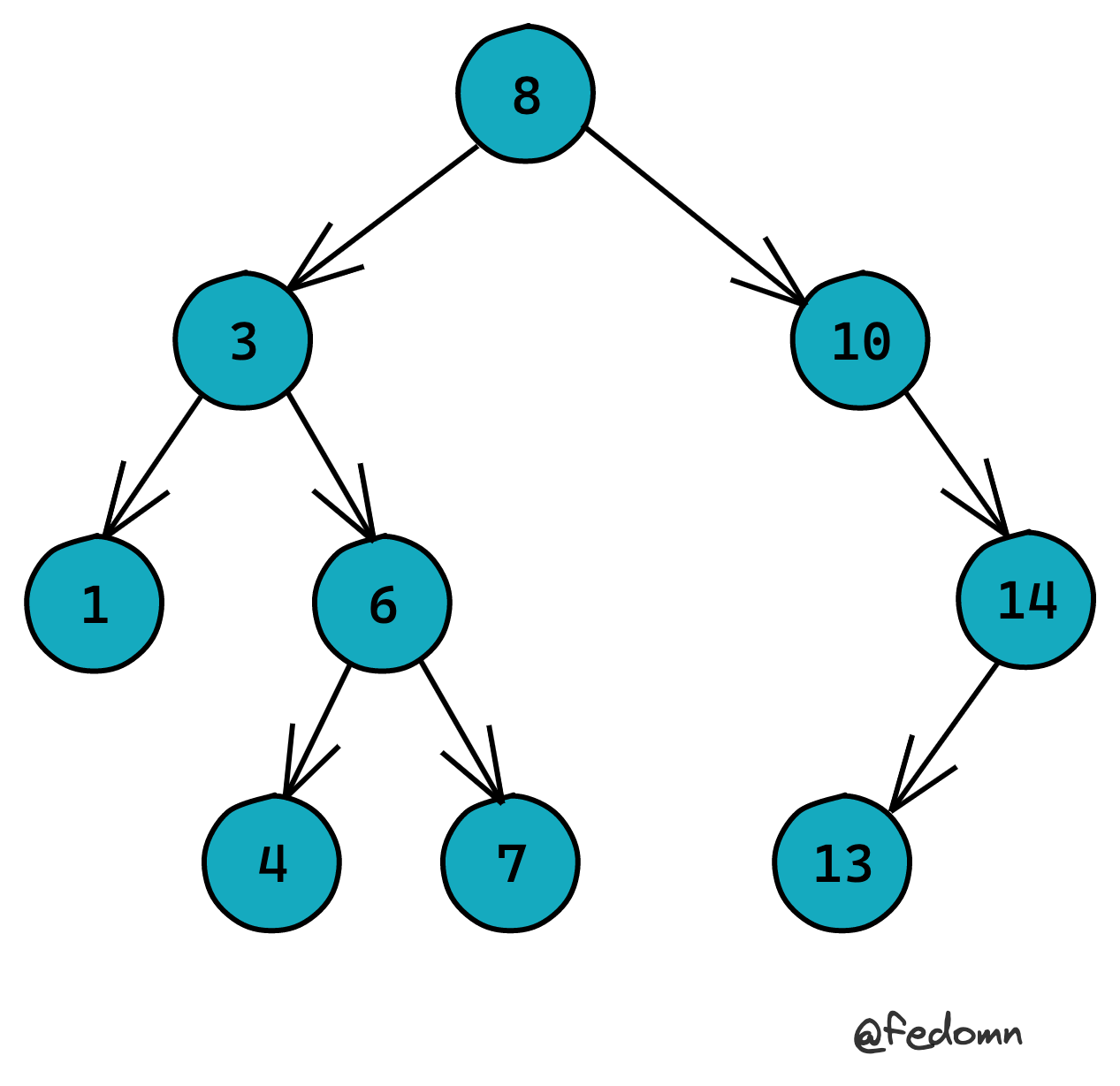
所以，当insert、search的时候只要从root二分查找到位置就好，但是delete情况下，要分如下情况：

1. 删除没有children的node，如1：直接remove
2. 删除有1个child的node，如14：remove 14再用13代替它的位置
3. 删除有2个children的node，如8：开始前要理解tree的in-order遍历。 这里有两种选择，取8在in-order数组中的predecessor或successor。即比8小一个的值(left sub-tree里的最大值)，或比8大一个的值(right sub-tree里的最小值)。然后用它来replace 8。即上图中的7或10。

以上就是BST的删除操作，同时也引出了一个问题，unbalanced。即在删除有2个children的node时，你始终用in-order predecessor，或始终用in-order successor，最终会造成一个左小右大，或左大右小的树。有点像长短不均衡的两只手臂。产生的原因也很好理解，因为你始终只在一边取值来replace root。

unbalanced 带来了什么问题呢？

举例来说，一棵10个节点的树，树的高度越高，也就代表只有1个child的node越多，再逼近思考，就近似看成10个节点排序连接的链表，它的高度就是10。它的查询效率就近似于遍历O(n)遍历查询了。

Self-balancing binary search tree因此出现，它也称height-balanced。即所有叶子节点的深度趋于平衡，广义上说对树上的所有节点查询的复杂度，平均起来偏低，也就是我们说的logN。它解决不平衡的手段是：每次插入或删除后进行平衡。比如插入造成分支不平衡，则围绕中间节点进行旋转，中间节点提升为父节点，原来的父节点则变成了右子节点或左子节点。而删除造成的不平衡，可能需要merge/borrow操作。可以等下参考B-Tree。

最后总结一下，BST搜索的复杂度，最差为O(N)，最好为O($log_2N$)。

Paged Binary Trees

最终我们需要将BST写到磁盘上持久化起来。面临的主要问题：locality。解释成，如何在磁盘上快速取出某一节点。

所以必须考虑读写HDD(Hard Disk Drive)和SSD(Solid State Derive)性能。先粗浅理解，HDD是由磁头机械寻址读写一块地址，SSD是由控制器寻址。它们都是一种块设备，需要逐块读写。

(SSD特别之处：直观感受它的随机读写效率应该很高， 但是SSD顺序读写性能仍然是高于随机读写的。原因我们粗浅理解为连续读写存在预读优化，不论内存还是磁盘，连续读取可预见的操作有优化空间。)

因此自然得出，减少I/O操作 和 采用顺序读写 来操作磁盘。

而BST的扇出很低(2个)，叶子节点深度就会很深。所以，如果要保证插入的新节点和父节点在一个page上，可能比较复杂。查询也是同样道理，尽可能的让一次I/O操作拿出很多节点。

考虑这些问题，需要设计出的BST满足：高扇出，低高度。

B-Tree

The ubiquitous B-Tree paper介绍了B-Tree和它的变形体。同时需要统一话术，节点是指具体的kv，而node是指逻辑上的一个page可包含多个节点。

我们上面说到，数据需要读写如何快速找到读写的位置，我们需要BST。而B-Tree就是一种self-balancing的BST，它扩展了BST，允许一个node可以多个keys和children。而这么做的原因，是为了让一个node可以容纳下更多的keys，这样存储系统的一个block里，能够存放更多数据。提高的读写效率。所以，它广泛用于数据库和文件系统。

B-Tree满足了搜索(BST)和读写(磁盘)的要求后，如何做到的self-balancing，让所有key的深度趋于平衡。

首先了解B-Tree的node：

• Internal nodes：包含除了root和leaf以外的所有nodes。它内部包含一个ordered set of elements(kv组合)和child pointers。每个element看做是BST里的一个key，用来分隔左右subtree，这里是左右child pointer。所以，count(element) + 1 = count(child pointers)。
• Leaf nodes：它只存储数据(kv组合)，没有child pointers。
• The root node：类似internal nodes，它和internal node一样有最大element限制，但没有最小element限制，也就是说它可以没有children。

这些nodes组合下的B-Tree满足特点：

1. 每个node最大能有2*t-1个keys. 理解为：2*t-1 = (t-1)左半部 + (t-1)右半部 + 1(spilled节点)
2. 每个node最少有t-1个keys (expect root)
3. non-leaf node包含t-1个keys，也就会包含k个child pointers
4. 所有leaf nodes都存在于同一层
5. B-Tree grows and shrinks from the root which is unlike Binary Search Tree. Binary Search Trees grow downward and also shrink from downward. 理解为：B-Tree的插入删除都是从parent node进行操作，也就代表，在从root->leaf node的路径中，遇到不满足特点的node，及时进行修复后，再执行插入删除。这就是B-Tree的秘诀：在查询的路径上，解决掉不满足约束的node。优势：在查询节点的同时执行了操作，相比于先找到leafNode再自上而下影响父node，减少了回溯的block操作。

根据这些概念有如下B-Tree example：它的t=2，所以node maximum degree=3，node minimum degree=1

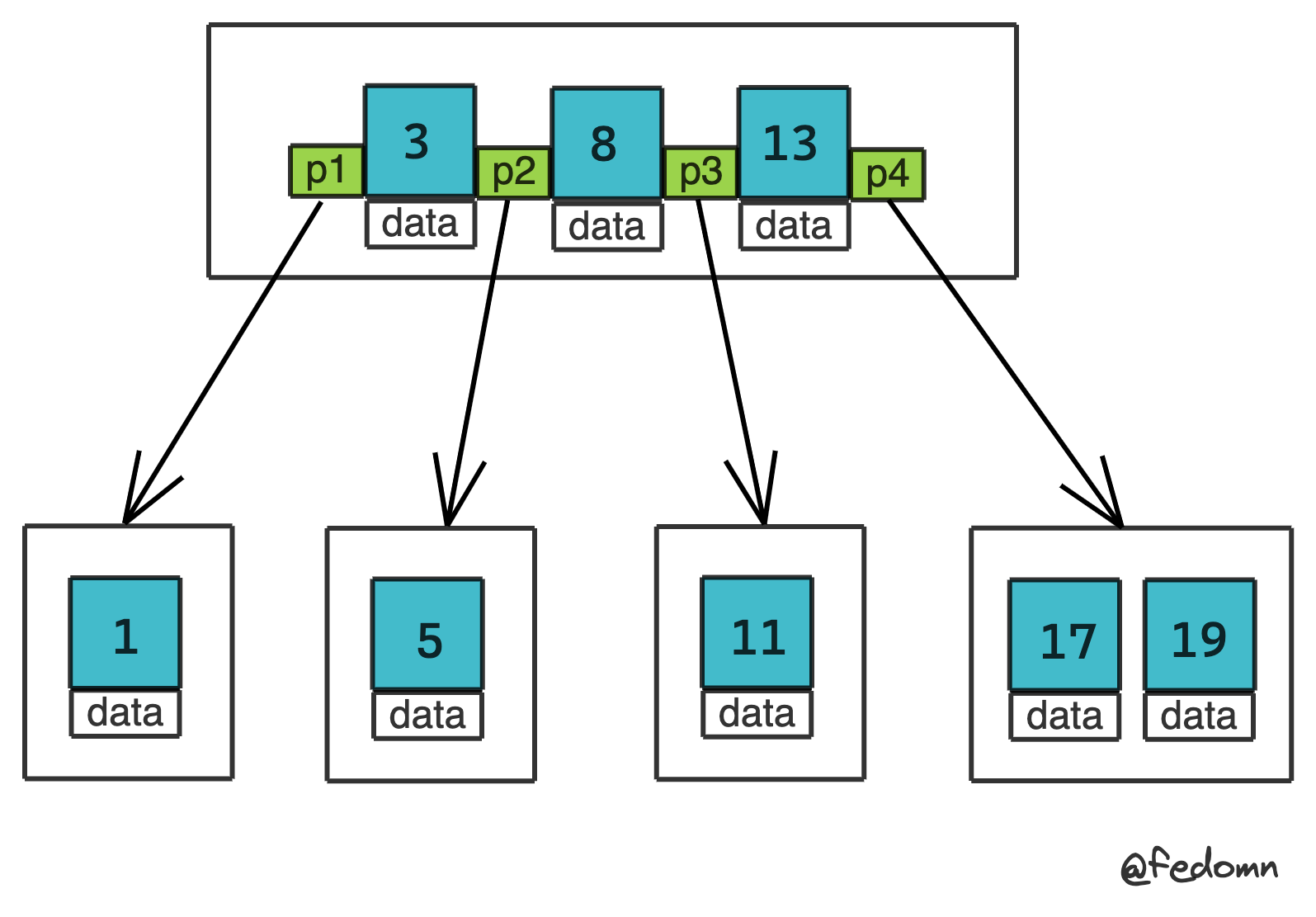
下面从查询/插入/删除来理解B-Tree平衡操作

a: 查询时：从根节点执行二分搜索，通过搜索key比较来定位数据最终的叶节点或内部节点

insert

b: 插入时：从root往下search，经过一个parent node时，如果发现将要去的child node里key个数 = maximum degree值，则将该child node分裂成两个node，并将分裂的spilled key提升到当前所在的parent node中，

如上图它的t=2，node maximum degree=3，node minimum degree=1，当insert key = 22时，它的执行步骤：

1. 从root node开始search，发现root node keys full，则执行splitChid操作
2. 原先root node作为left child，新增一个right child从left child copy t-1个keys，即left保留3，right新增13
3. 将spilled key 8放到新增的root node里，至此结束search path路径上的第一次平衡
4. 继续插入22，通过parent keys比较下一步插入node是13所在node
5. 发现13所在node not full，则继续往下找到17,19所在node，进行插入
6. 插入22后所在node，结束插入操作

insertion伪代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

func (n *node) insertNonFull(key int) {
	if n.isLeaf {
		// insert into node
	} else {
		// if child already full, will splitChild
		if n.children[idx+1].isFull() {
			n.splitChild(idx+1, n.children[idx+1])
		}
		
		// insert correct child node
		n.children[idx+1].insertNonFull(key)
	}
}

remove

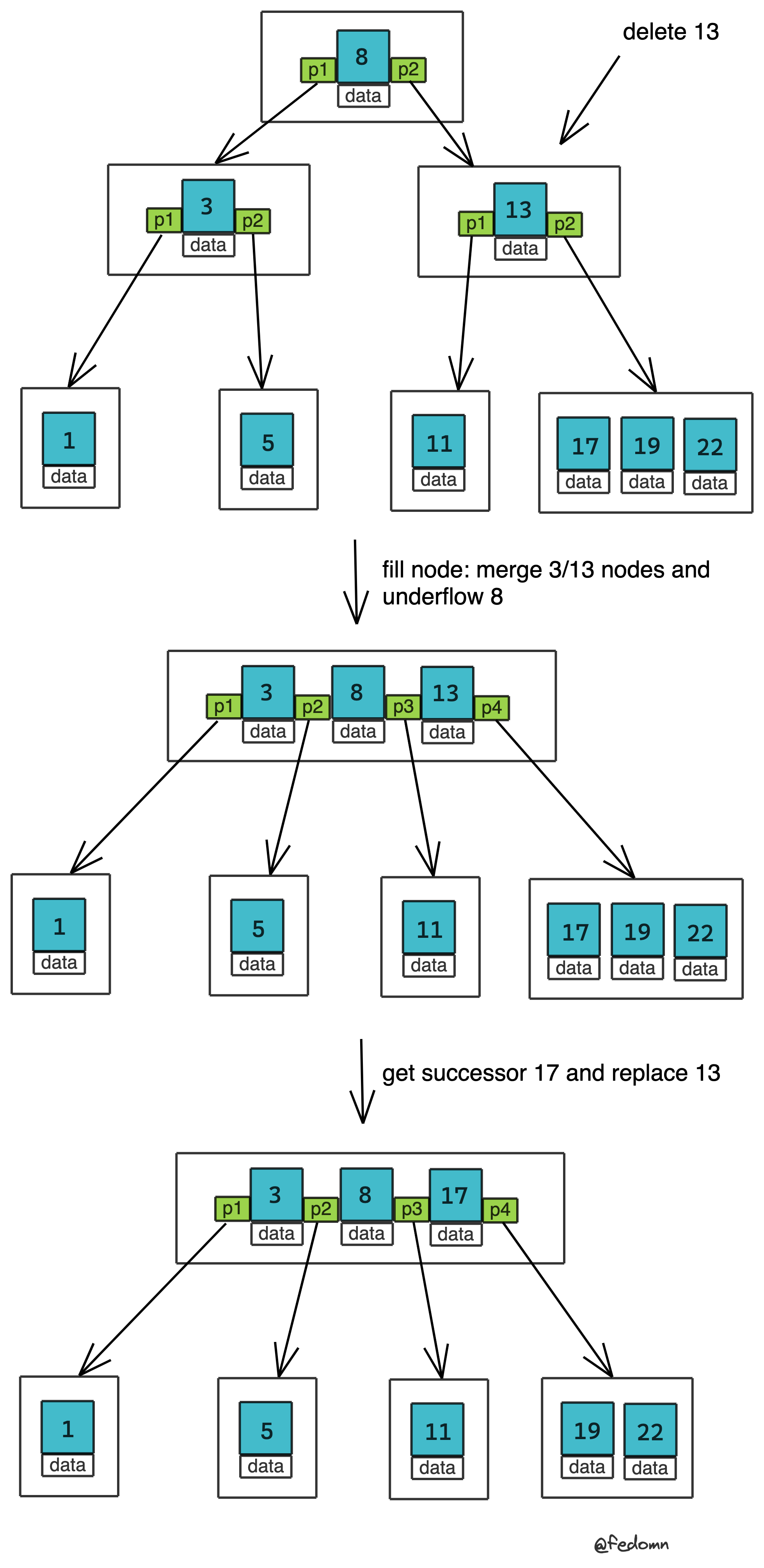
c: 删除时：从root往下search，经过一个parent node时，如果发现将要去的child node里key个数 = t-1 (即可能在删除一个key后，不满足最少t-1个数要求)。则及时将该node修复(borrow/merge)，再递归向下搜索key并删除。 具体分为以下两种情况：

leaf node：则直接在leaf node删除该key

internal node：分两种情况，key在该internal node上；key在该internal node的child里。

c.1：key在该internal node上。

c.1.1：如果node的left child >= t，则取该node前驱最大值predKey，来replace删除的key，再从left child开始递归的删除predKey

c.1.2：如果node的right child >= t，则取该node后继最小值succKey，来replace删除的key，再从right child开始递归的删除succKey

c.1.3：左右child都 < t，则执行merge，将right child keys 移动到 left child node，再将删除的key下溢到left child node，最后从left child里删除key

c.2：key在该internal node的child里。

这种情况下，需要从parent node递归往下查询，遇到不满足最少t-1个数的node，及时填充node，为删除后仍然满足minimum keys count = t-1 做准备。

c.2.1：在fill阶段，如果left sibling node >= t，则从左兄弟borrow一个key到parent node，再将parent node key underflow到待插入node。

c.2.2：在fill阶段，如果right sibling node >= t，同理左兄弟相同操作borrow and underflow

c.2.3：在fill阶段，左右兄弟都不满足 >= t，则需要merge 左右兄弟，类似c.1.3操作。

注意在fill填充完后，node keys 个数 = t，为后续remove一个key后，node keys仍然>=t-1做准备。

remove伪代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

func (n *node) remove(key int) {
	idx, found := n.find(key)
	if found {
		if n.isLeaf {
			// 直接从leaf node删除key
			n.removeFromLeaf(idx)
		} else {
			// 取前驱值/后继值/merge后，再删除key
			n.removeFromNonLeaf(idx)
		}
	} else {
		// 如果node keys个数 <= t-1，则要进行fill，为后续remove key后，仍然满足最小key个数准备
		if !n.children[idx].overMiniDegree() {
			n.fill(idx)
		}

		// 递归往下remove
		n.children[idx].remove(key)
	}
}

举例来说，如下图删除13：

B+Tree

BTree由于non-leaf node可以存key+value，导致在一个block里可以存放的kv数量大大减少，从而增加了BTree的层数，造成了查询block次数增多，时间与IO操作都会增加。

B+Tree解决这一问题，通过只能在leaf node上存放节点kv，而non-leaf node只存放节点k，来增加了non-leaf node存放节点个数，减少BTree层数。同时leaf node之间相互link，对外提供了有序访问。

因此，B+Tree的leaf node构成了索引的第一层(顺序通过key找value)，non-leaf node构成了多级索引的其他层。leaf node中的key同时也存在于non-leaf node中用于搜索。

B+Tree相比BTree最大的区别：

• BTree里key的value可以存到non-leaf node上，而B+Tree只能存到leaf node上
• B+Tree中leaf node中的key，同时也存在于non-leaf node中

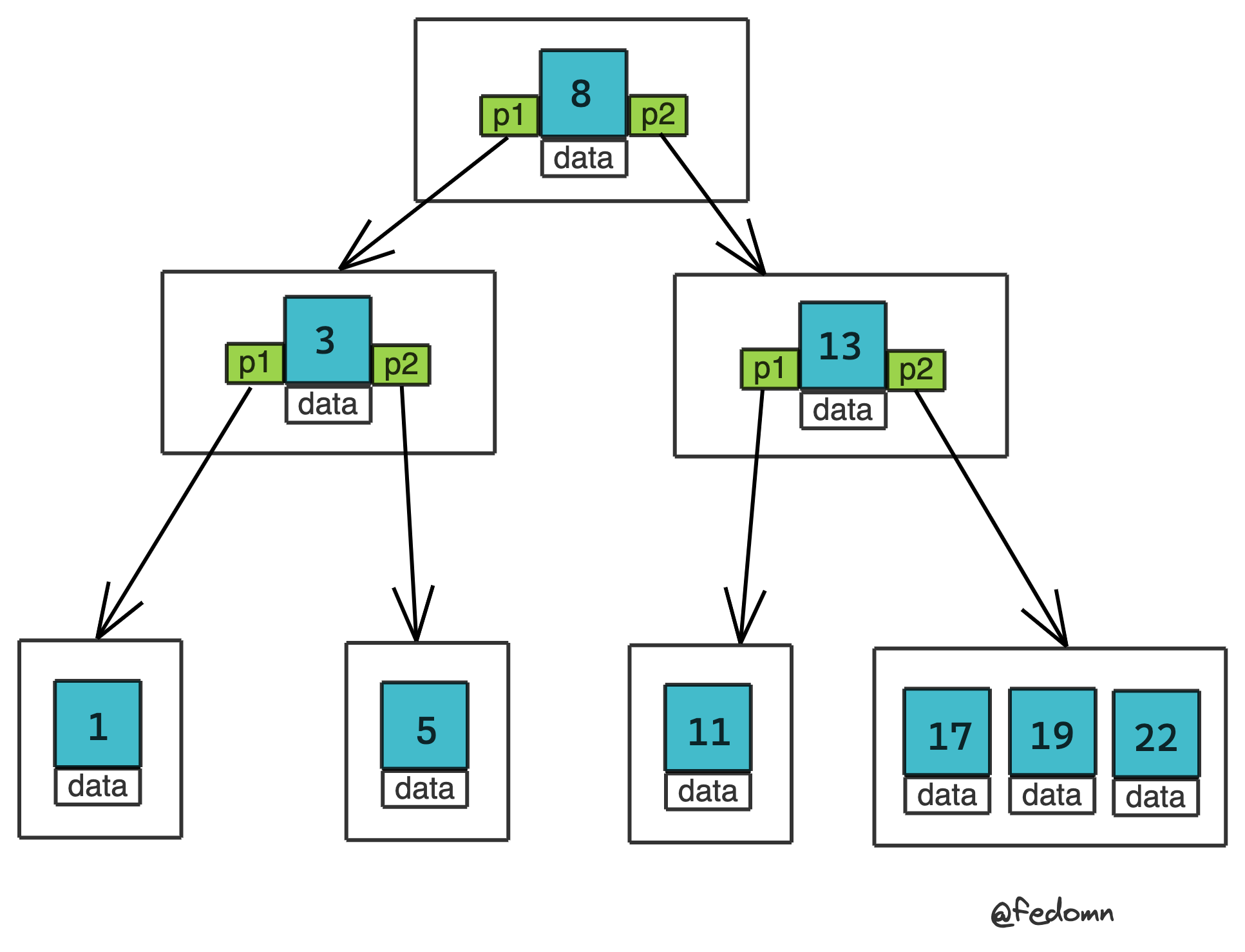
insert

B+Tree的插入操作和BTree类似，splitChild时机一样，区别在于：一个kv最终要插入到B+Tree leaf node中。所以在splitChid leaf node时，保留spilledKey到rightChild，但在splitChild internal node时，还保持BTree一样。 同时每次在splitChild leaf node时候，记得更新next指针。

如下图：

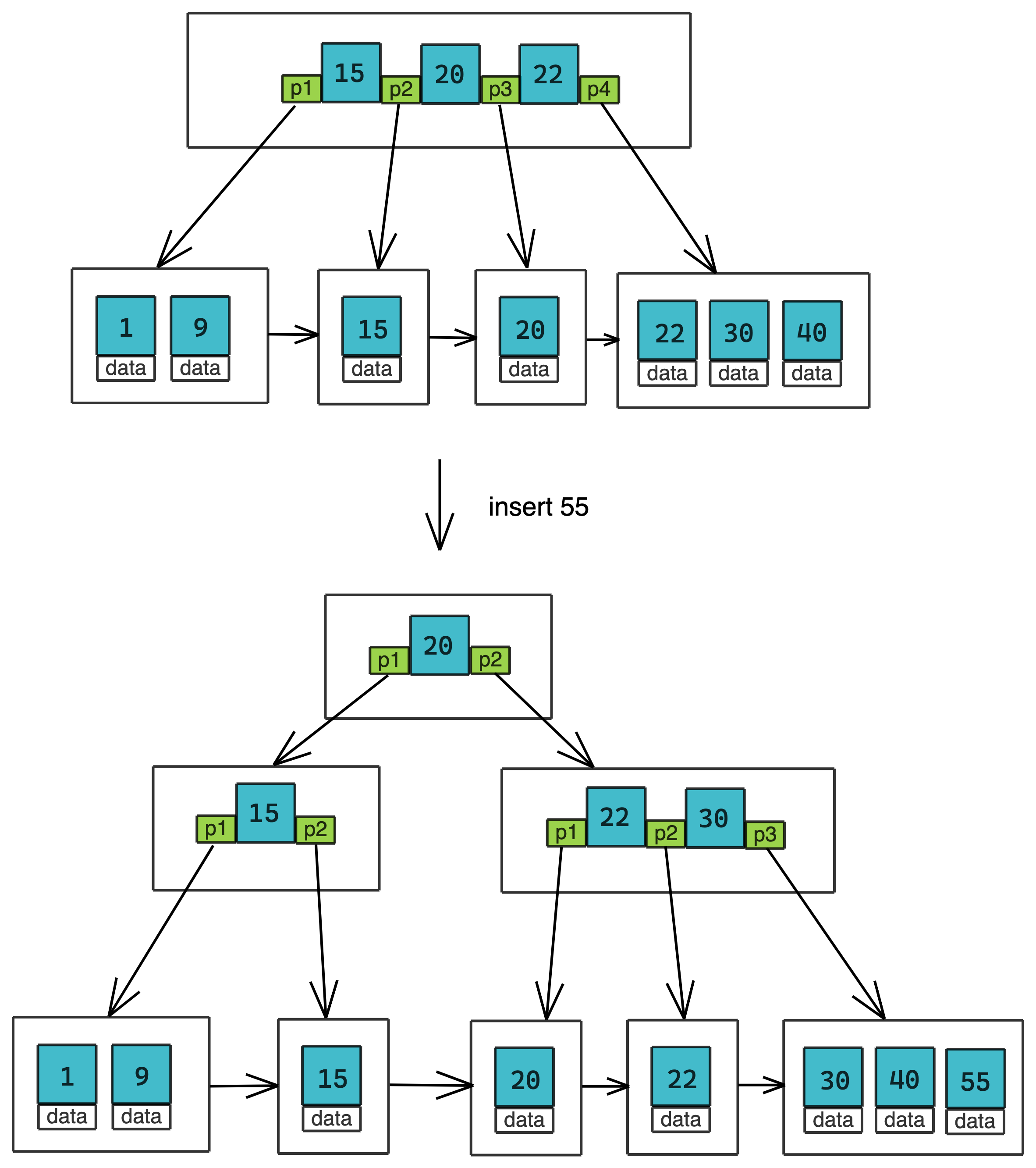
remove

B+Tree删除一个key最终要在leaf node上执行remove，但是non-leaf node上的key作为辅助的定位的索引，不会被删除。

B+Tree相比BTree的remove，有如下特点：

• B+Tree没有removeFromNonLeaf操作，因为所有remove都发生在leaf node上
• B+Tree的borrow操作对internal node来说和BTree一样，但B+Tree对于leaf node的borrow操作，注意的是：不能用internal node的key下溢插入到leaf node中，而应该用borrow的left/right node中的key来补充leaf node
• B+Tree的merge操作，也是要将internal和leaf node来分开，如果是internal node操作和BTree一样，如果是leaf node则不用下溢操作，直接copy right keys to left node

通过代码角度来说，B+Tree相比BTree，remove操作核心的不同就是：

• borrowFromPrev 和 borrowFromNext中的underflow操作
• merge中的underflow操作
• 没有removeFromNonLeaf，只有通过fill函数来平衡node个数

所以，总体看来B+Tree比BTree简单一些，这里就不画图展示remove过程了。

总结

自上而下

真正在实现B+Tree算法时，可能会很困惑，因为许多资料都会告诉你：它是一个自下而上影响的树，所以代码实现起来也是自下而上更新，当然许多教材伪代码也是这么实现的(如下emory资料)。

但是，实施起来通过child去更新parent里的key和pointer，并不容易，比如：回溯操作(记录parent指针)，node不满时填充操作等。

换个思路，这些操作从parent发起，并且在自上而下的路径上，及时地执行平衡操作(遇到不平衡的internal node就立马解决)，而不是找到最底层的leaf node后回溯去解决internal node。

所以，就有了n.children[idx+1].isFull()判断；n.splitChild(idx+1, n.children[idx+1])操作。都是通过parent来操作child，也减低了remove操作中的borrow/merge的复杂度。

因为从顶层视角来看，通过parent操作children比较符合常规思维，方便理解记忆。

数组 or left/right指针

internal node有个child pointers，这里是通过一个数组去保存child pointers呢？还是通过给key一个left pointer和right pointer呢？哪种实现起来更方便？

实践下来，维护left/right pointer在insert阶段复杂度还好，但是到了remove阶段，复杂度就上来了，需要同时考虑left/right如何更新。

如果通过child pointers数组和keys数组来构造internal node，就需要有个隐含的关联：当key的idx=0，则它的left child在child-arr中idx=0，它的right child在child-arr中idx=1。

通过数组构建的方式，实践下来会简单很多。

测试

测试对于这种数据结构操作来说很重要，尤其是fuzzy test + benchmark来模拟随机操作过程。

BFS和preOrder也是分析测试必不可少的。

BTree Draw可视化也是快速反馈的方式之一。

代码

BTree golang

B+Tree golang

reference

• BTree动画
• codedump-B树算法原理
• geeksforgeeks BTree delete
• emory B+Tree insert
• emory B+Tree delete
• Implement Key-Value Store by B-Tree