Log-Structured Merge Tree

2021-06-28 7144 words 15 minutes

Contents

在上一篇介绍B-Tree变体中，我们得出：通过缓冲可以改善写放大和空间放大的问题。应用缓冲的方式有：推迟磁盘页的写入传播，以及写操作顺序化。

LSM树则使用缓冲和 append-only方式来实现顺序写操作。LSM树写入不可变的文件，并且随着时间推移将它们合并在一起。这些文件通常包含它们自己的索引，用来高效定位数据。尽管LSM树通常被作为B树的一种替代，但B树通常被用作 LSM树的不可变文件的内部索引结构。

LSM树的缓冲和append-only，实现了 写入推迟，数据的更新最终写入到不可变文件中。带来的优势：

相比B树可变的数据文件，LSM的append-only不可变文件，避免了随机写操作，同时LSM是append-only方式，也避免了数据碎片问题，具有更高的数据密度
由于不可变文件，也避免了CUD操作事先需要在磁盘上定位数据的问题，显著的提高了写入性能和吞吐量
LSM树的读和写互不交叉，所以在并发读写时，LSM使用数据和索引文件的内存视图，对它进行并发保护。而不需要像 B树可变结构采用latch和lock保证磁盘文件的数据结构并发读写。LSM通过这种方式简化了并发访问的复杂度

LSM-Tree Structure

LSM-Tree由较小的内存组件和较大的磁盘组件组成。

memory-resident组件是可变的，它缓冲数据，并作为读写操作的入口。当内存中大小达到阈值后，会持久化到磁盘中。当然对memory-resident的写操作也是由WAL日志保证durability的。

disk-resident组件，将内存中缓冲的内容flush到磁盘中。由于文件不可变性，它仅用于读取。

Two-Component LSM Tree

双组件LSM-Tree，它只有一个磁盘组件，由不可变段组成。参考上一篇的FD-Tree。这个磁盘组件被组织成B-Tree，同时具有 100%的节点占有率。

memory-resident子树的内容被分块写到磁盘上。在刷写期间，对于每个被刷写的memory-resident子树，都有一个disk-resident子树与之对应。它们最终合并后，会写入到新的磁盘段中。而合并前的，子树将会被丢弃。这种方式类似于之前介绍的CoW树。

如下图，灰色部分是flush的 mem和disk 子树

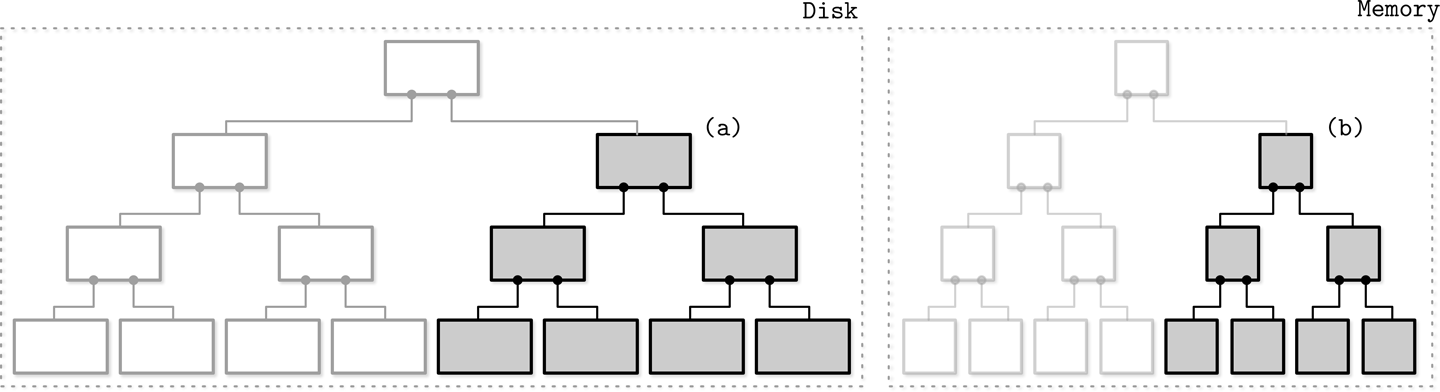
在实现子树 merge和flush 的要素有：

flush一旦开始，所有的新写操作，都必须转移到新的memtable中
在子树flush期间，mem和disk的子树都要保持可以被读取的状态
在子树flush完后，需要保证发布merge后新内容，丢去merge前mem和disk的子树，这两个操作是一个原子操作

特点：双组件LSM-Tree 会频繁地维护索引文件(mem和disk)，所以当每次memtable flush时，都会触发一次disk-resident子树的flush，避免不了的写放大。

Multi-Component LSM Tree

多组件LSM树，即它具有不止一个disk-resident表。每次memtable flush后，会产生多个disk-resident表，所以我们查询数据时，必须要访问多个文件来定位。

为了缓解从多文件读取数据的压力，需要一个周期性的compaction过程，将多个disk-resident表 compact成一个表。

如下图，memtable大小到阈值后，会flush到disk-resident表中，再经过compaction最后合并出更大的表

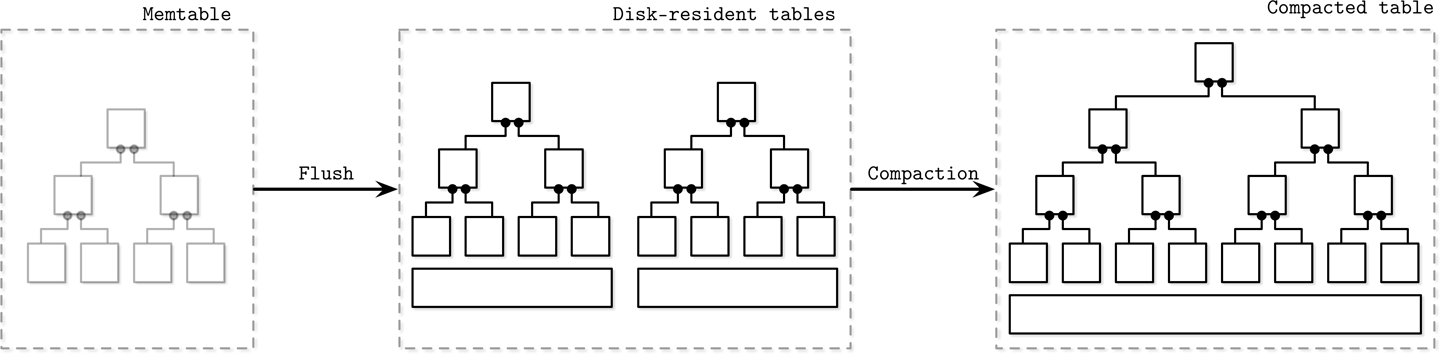
memtable

flush memtable到disk时前，必须分配一个新的memtable 用来切换，让它成为新的写操作目标，而旧的memtable则转变为flush状态，这个两个操作必须被原子性执行。

当memtable完全被flush到磁盘后，会生成一个disk-resident的table用于读操作，而该旧的memtable会被丢弃，取代它的是一个新的memtable。

如下图展示了 memtable 到 disk-resident表的转换过程。

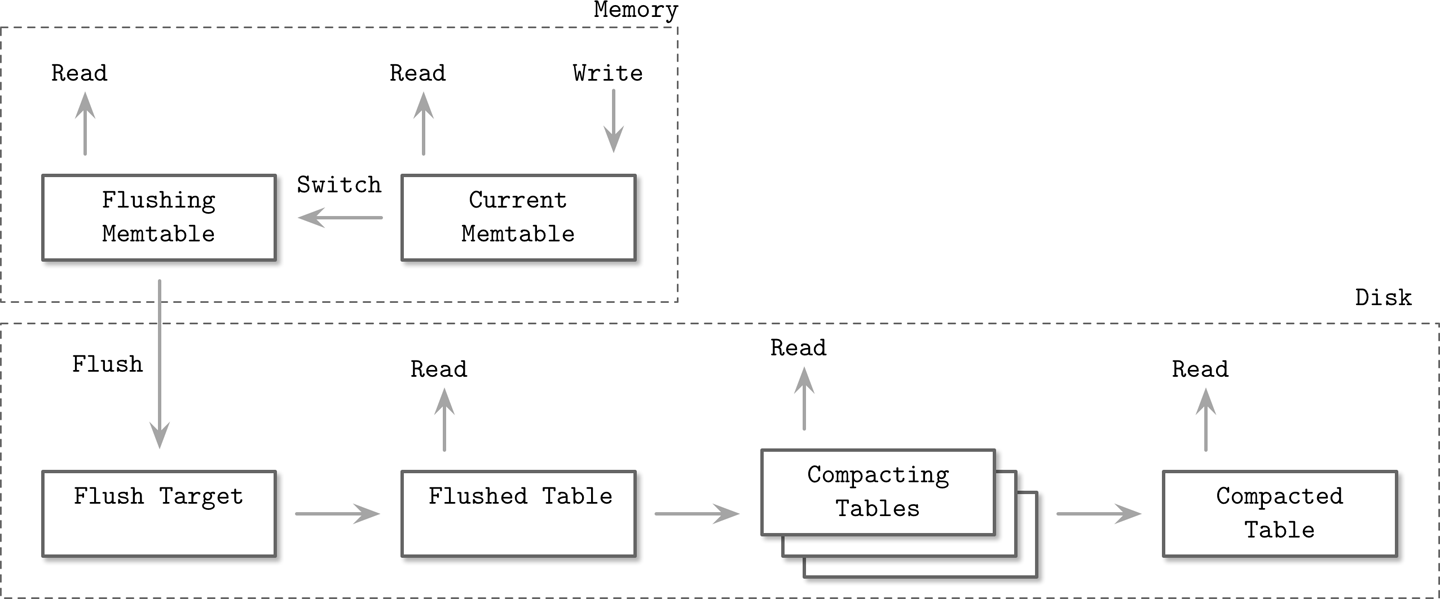
其中有两点：1. 数据在memtable是经过排序后的，所以可以依次写入disk-resident表中，不论对disk上的数据结构还是I/O都会有很高的效率。2. 在flush memtable之前，其内容的唯一持久化地方是WAL，当memtable完全flush后，其对应的WAL就可以trim处理，丢去已经flush的那部分log。

更新与删除

由上面的LSM-Tree不可变磁盘文件，可以知道，对insert / update / delete操作不需要在磁盘中定位数据。但是对于读取操作，则需要对冗余数据进行reconcile。

这个reconcile过程很类似之前说的FD-Tree，当delete一个key时候，通过插入一个Delete Entry表明，该key逻辑上已经删除了。

对于删除范围keys的操作来说，需要通过 predicate deletes(谓词删除) 来标记。该predicate通常是根据排序规则来的，如: **delte from table where key >= “k2” and key < “k4”**的形式，对于了两个Delete Entry。[k2, >=] 和 [k4, <]。Apache Cassandra称其为 range tombstones (范围墓碑)

也就说有了这两个entry，在从下往上 reconcile 表时，遇到匹配到predicate的数据记录，将会被跳过，不返回给客户端。

Merge-Iteration

LSM树由多个组件构成，查找过程则需要访问多组件，所以在返回给客户端之前，必须对其内容进行合并。

由于LSM的disk-resident表是排序后的，所以在merge的时候，可以通过merge-sort归并排序算法。

iteration迭代器是指，disk-resident / memtable 提供的一种游标，来遍历文件内容。所以，merge-sort是对这些iterator进行merge排序。

核心是：构建一个优先队列。该queue包含N个元素，N为iterator个数。该queue每次返回其中的最小元素，即一个iterator的head值。当queue取出一个元素后，会继续从iterator取下一个值，放入queue。如此反复执行，直到iterator里元素取尽。

这样保证了，merge后依然保持了有序地输出元素。如下图

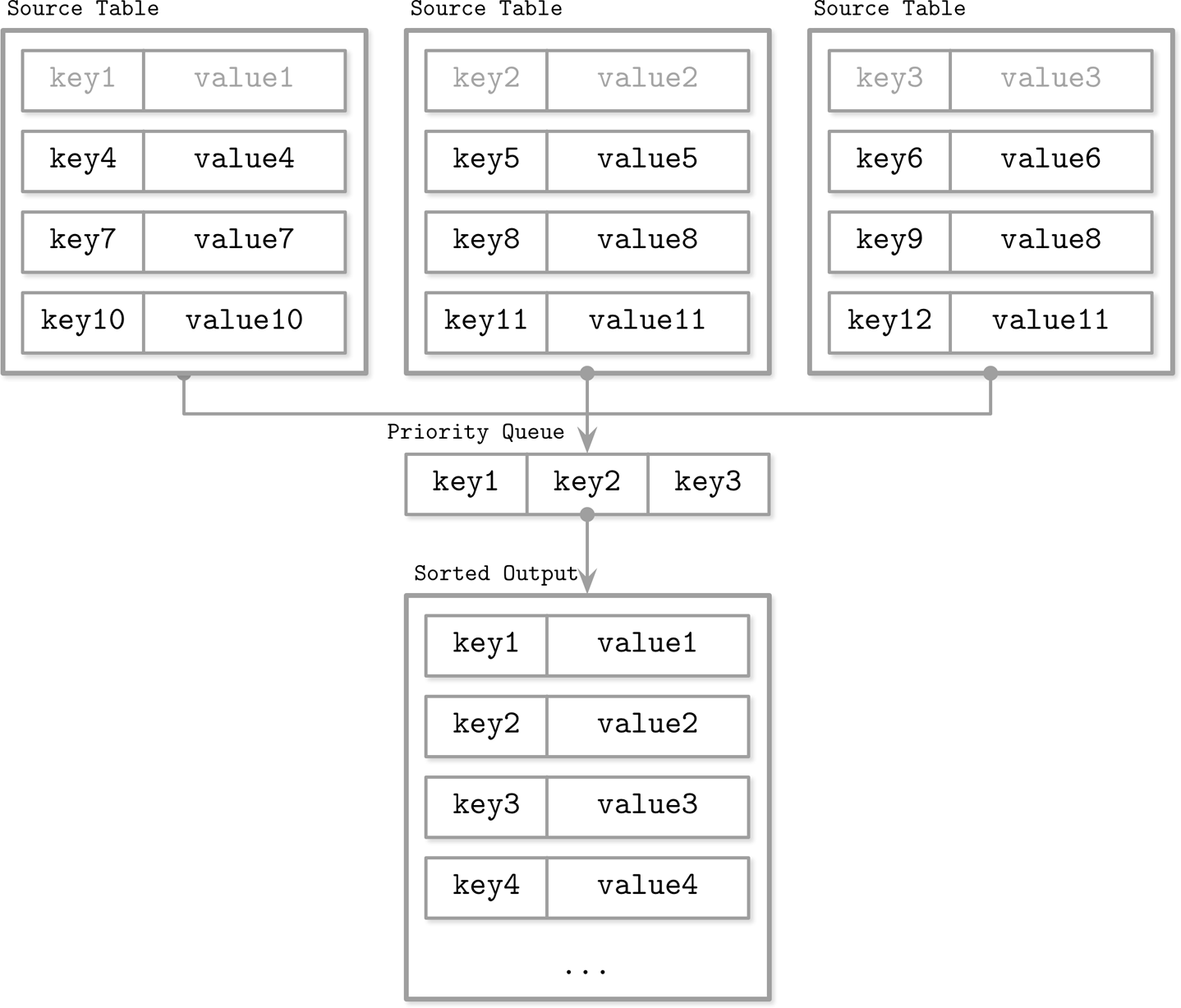
reconcile

reconcile需要解决的是，多条相同key数据的冲突，需要知道哪一条是最高优先级的。

因此，在记录数据时候，需要保持一些metadata用来判断。比如时间戳信息。

更大的时间戳数据，代表最新条数据，它会隐藏到时间戳小的数据记录。

compaction

LSM树中，disk-resident表数量会不断变多，所以需要周期性地compaction来触发merge，写入结果到新创建的表中。

compact特点：

存在一个内存上线，即构建priority queue的内存大小，上线 = N x 一个元素的mem
磁盘需要保证有充足的空间，用来写入compacted后的表
compact操作同时并发操作多个表

Optimization: leveled compaction

通过分层compact方式进行优化，RocksDB采用这种策略。

核心：disk-resident tables 被划分为多个level。每一层都有数据量大小的要求。

Level-0：由memtable直接flush创建的。因此，0层中各个表，可能包含key range的重叠部分。如t1表的key range=1~100，t2表的key range=50~100。这是因为是直接从memtable生成的，没有经过merge。

Level-1：1层和更高的层上的表，不会存在，key range上的重叠。因此，在compact时，必须将0层的表，分区后对相同key范围的表进行merge。

当一个层中表大小或表数目达到阈值后，就要进行跨level进行merge。如1层达到阈值需要 merge到2层，则会将1层中的一个t1，在2层中找重叠的key range表，将它们进行merge。如下图

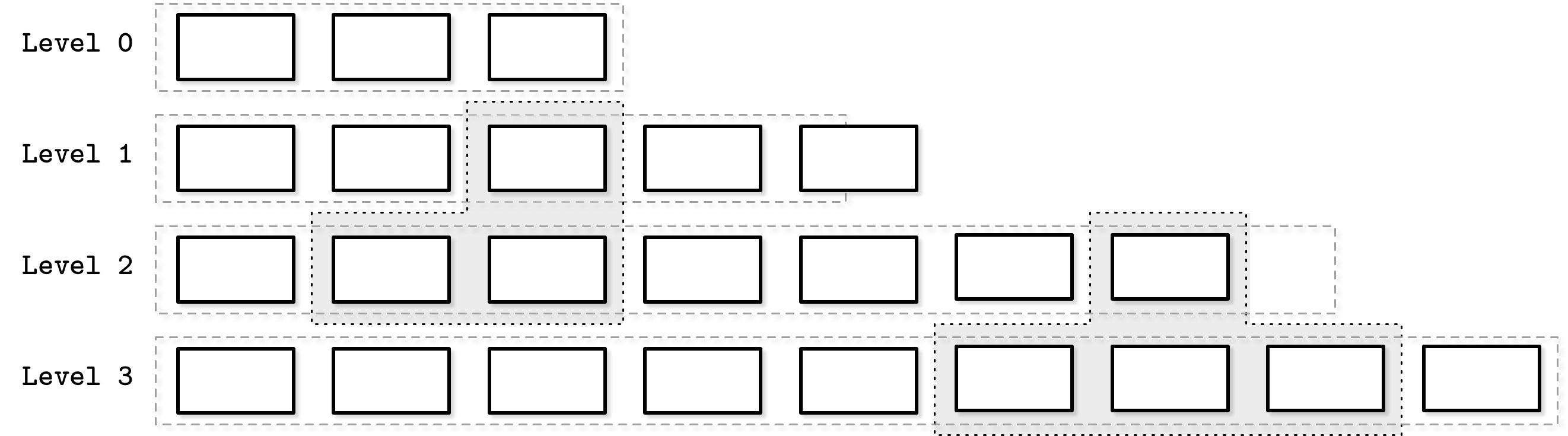
还存在一些其他的 compaction策略，针对不同的工作负载。比如，Apache Cassandra实现的a time window compaction strategy，它对于(time-to-live)类型的时序数据库来说很友好。因为，数据记录会在一定时间后过期，基于时间窗口的compaction策略，会直接丢弃已过期时间的数据，而不需要compact。

读/写/空间放大

在实现最优的compaction策略时候，避免不了需要考虑到读放大、写放大和空间放大，这三个因素。

LSM树中，为了回收重复数据占用的空间，以减轻空间开销，则需要经常merge表，但这又会导致写放大，如果减少merge表的频率，则又会导致读放大，需要读取多个表以reconcile数据，也会导致空间放大。

总结，基于immutable files存储数据时候，面临以下问题：

读放大：为了检索数据，需要读取多个disk-resident tables，在reconcile
写放大：compaction过程，需要不断对disk-resident tables进行重写
空间放大：immutable的特性，同一个key数据可能会被存储多次

存储结构的开销模型需要考虑三个因素：Read Overhead / Update Overhead / Memory or Storage Overhead

这是一种最朴素的猜想，同时优化其中两项，避免不了另一个项 overhead 恶化。而然对于分布式数据库，除了这三点，还包含其它需要考虑的因素，如一致性成本，复制开销等。但这个朴素的开销模型，有助于我们理解 存储引擎必须提供什么

参考 rum-conjecture

实现细节

SSTable

如何实现 immutable disk-resident，以满足有序性。通常使用 有序字符串表，即Sorted String Tables。

SSTable通常由：索引文件和数据文件组成。

index files 通常以类似B树或 HashTable查找复杂度类似的结构，来实现查找。它保存着key在数据文件中的offset。
data files 以key的顺序保持记录，同时它一旦写入则不可修改

由于data files中key的有序存储，所以即使hash索引也能满足范围查询，只要通过hashtables定位到range的第一个key，再根据range查询的谓词，向前或向后顺序取出数据即可。

SSTable-Attached Secondary Indexes

这是Apache Cassandra中实现的，SSTable附加二级索引。允许除了PK之外，其它任何字段来索引数据文件。一旦memtable flush到disk-resident tables时，对于的主键索引和二级索引也会创建出来。并且与SSTable具有相同的lifecycle。

如下关于SSTable的直观感受

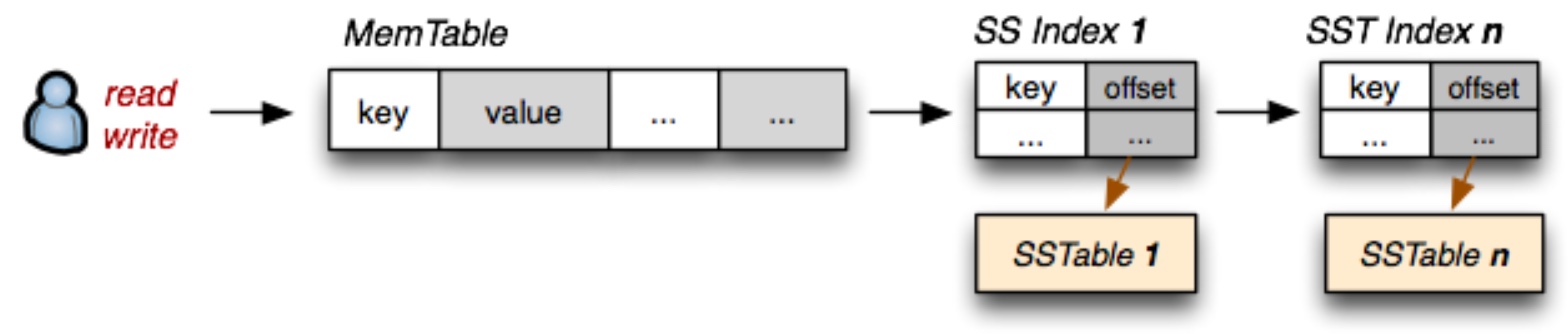
Bloom Filter

LSM树读放大原因，需要搜索多个disk-resident tables来定位数据，如果事先知道一个disk-resident tables是否包含要搜索的数据，就可以一定缓解读放大情况。

存储这个信息比较容易，只要给每个disk-resident tables标记是否包含某个index key，但这种方式会耗费大量的空间去标记，为了兼顾空间效率，Cassandra和RocksDB都采用了 概率型数据结构，Bloom Filter。

概率型数据结构允许我们不必精确存储所有集合，而是提供一种近似的结果，这样极大的提高了空间效率。如Bloom Filter。

布隆过滤器，用来测试元素是否属于一个集合。它可能产生 false-positive 情况，但不会出现 false-negative情况

false-positive：元素在集合中，但实际上该元素不在集合中
false-negative：元素不在集合中，则该元素 肯定不在 集合中

所以，只要使用 false-negative特性，过滤掉 肯定不在 集合中的tables，只访问剩余的tables，就可以极大地减少了访问表的数量。如下图

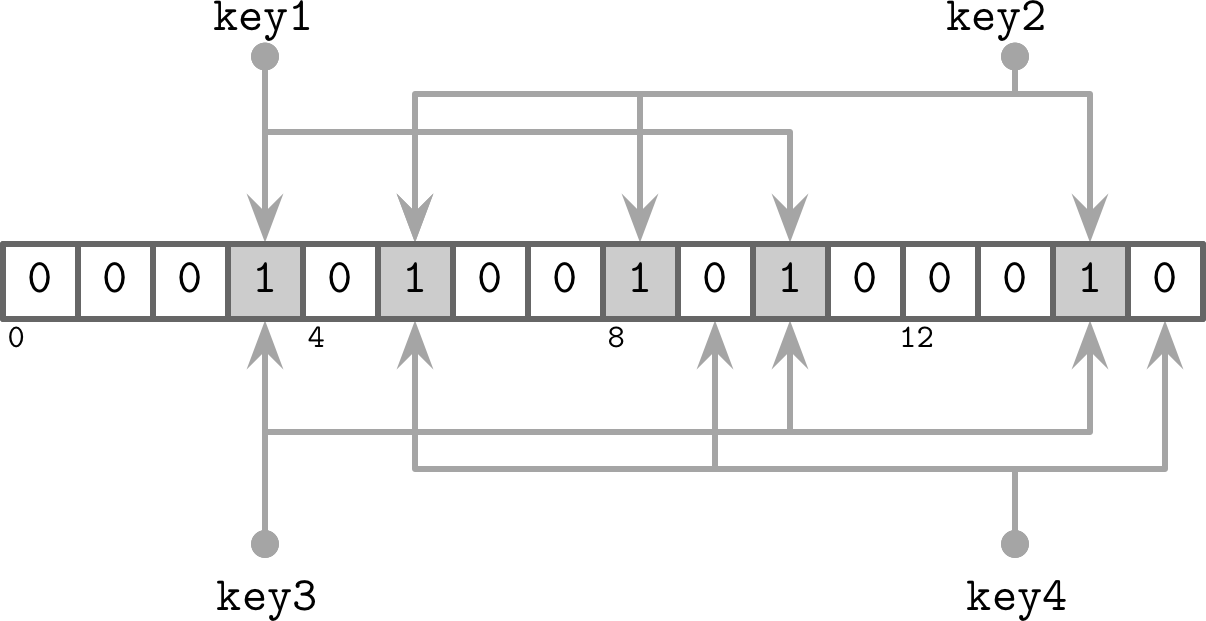
Bloom Filter = 大的Bit Array + 多个Hash函数

如上图中存在 3个hash函数，对key1分别求值，得到3、5和10。就会在Bit Array对应的index上标记为1。像这样重复求值key2/key3/key4，所以如果Bit Arrray里的index=3的位置=1，只能表示key1可能存在，因为key3也会在一个bit上标记。

所以，不同key值经过hash函数计算后得到相同值，就导致了hash冲突。为了避免，加大Bit Array，提供更多Hash函数。但这也会相应带来，内存与计算性能的负面影响。因此，需要相互权衡。

但是，因为LSM树中的表是immutable的，所以tables的key个数也是可以确定的，因此可以通过计算得出冲突概率，进而权限。

Skiplist

目的：内存中 保存 有序数据。

Skiplist 最初来源于Paper Skip Lists: A Probabilistic Alternative to Balanced Trees

从标题看出，它的初衷为了代替平衡树。我们知道，B-Tree在更新/删除节点后，可能需要旋转/移动节点，带来写放大负担，尤其是并发场景下，一次更新需要lock到较多节点，降低了并发性能。

skiplist本质类似一个 linked-list 带有 additional pointers，如下图带有指针的各种linked list

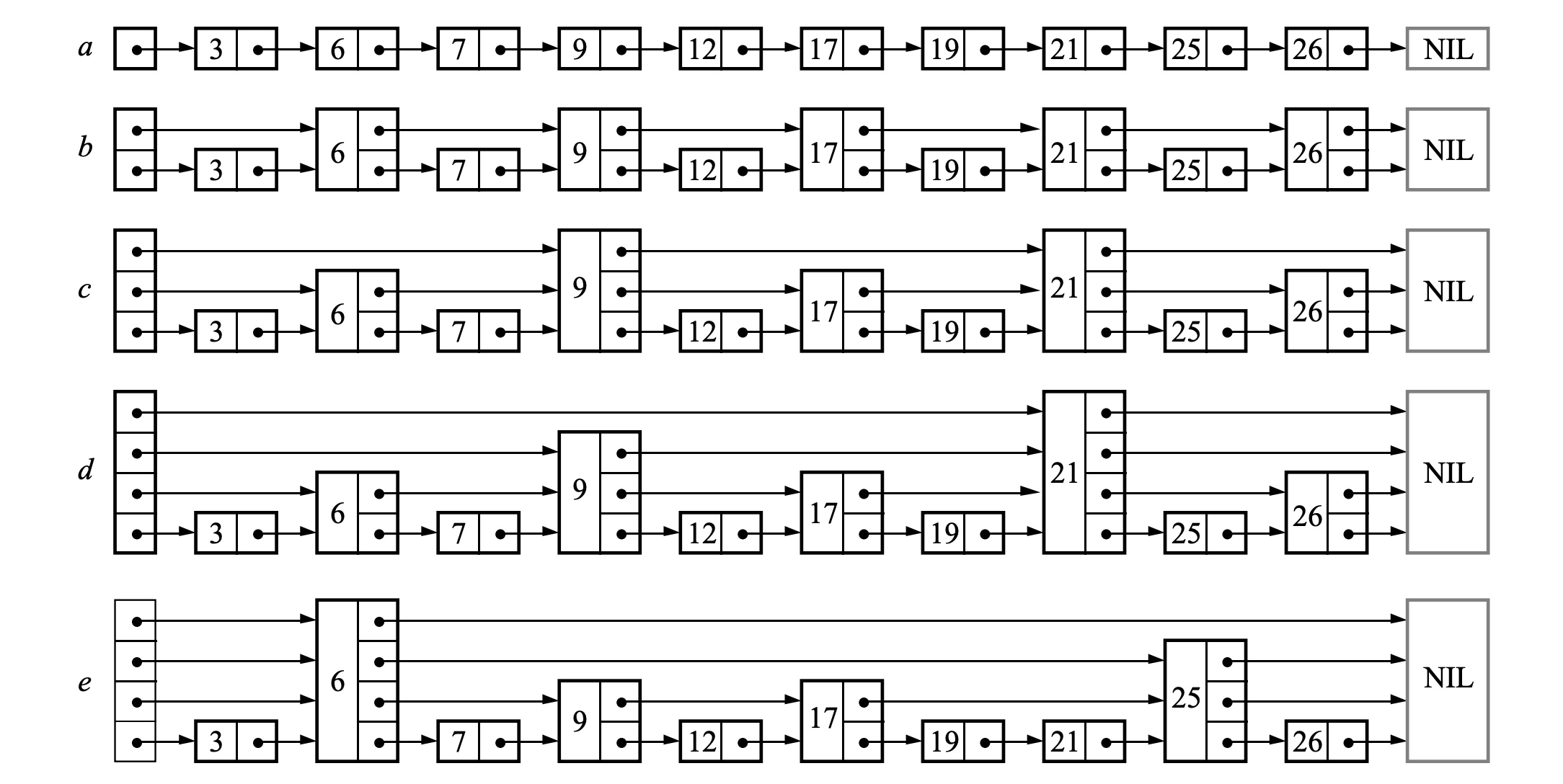
跳表具有简单的结构，类似linked-list，由一系列高度不同的节点组成，构建了链接在一起的层次结构，节点的高度由 基于概率分布生成的随机数来确定。如下图

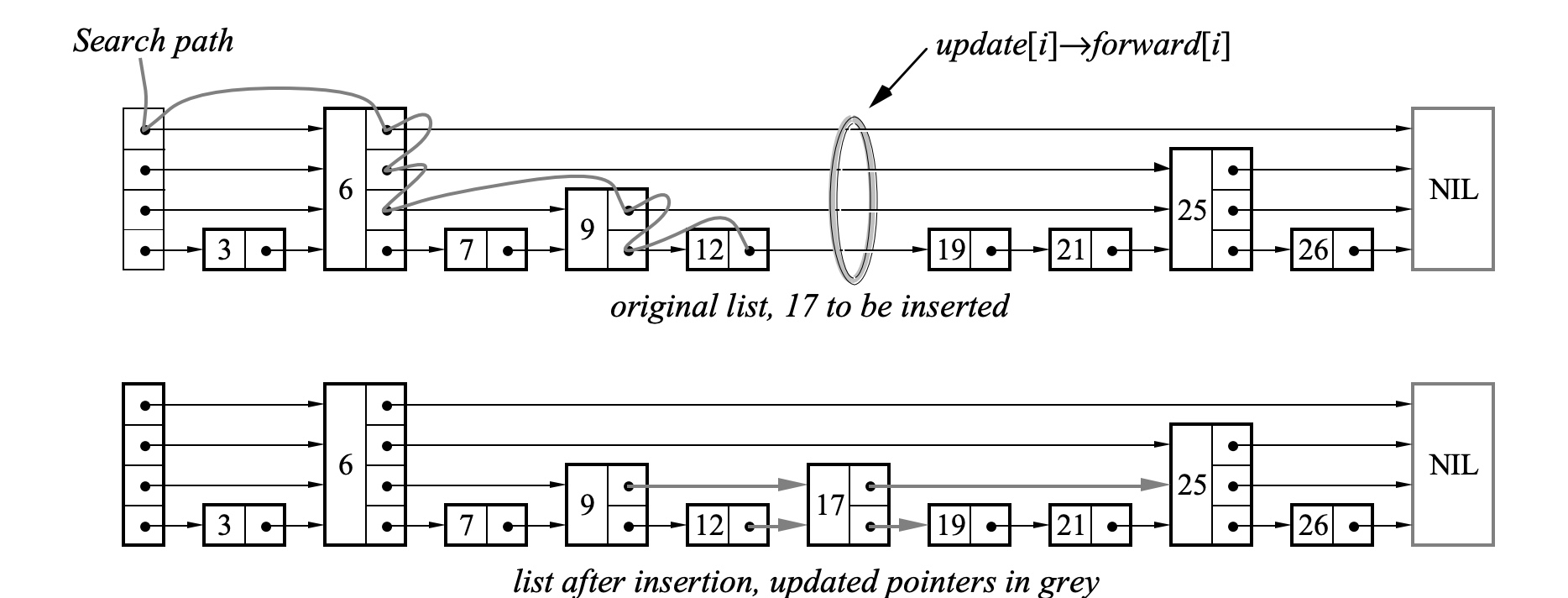
核心：search过程，从上到下一层一层找到 forward指针指向的key，判断与查询key大小。

如何根据概率分布得出节点高度呢？

需要2个常量：maxLevel表示元素最多可以有多少个向前的指针，它决定了skiplist的容量。p是一个概率因子，它决定了随机生成level的大小分布。如下图，p值对检索时间和节点向前指针个数的影响。检索时间代表了时间效率，节点向前指针个数代表了空间存储，两者对立关系。它的理论复杂度：O(log_level(N))。按照默认 level = 32 来看，当 N > 2^20 的时候，理论上 skiplist Get/Set 平均 4 次查询，而二叉树平均得 20 次了。

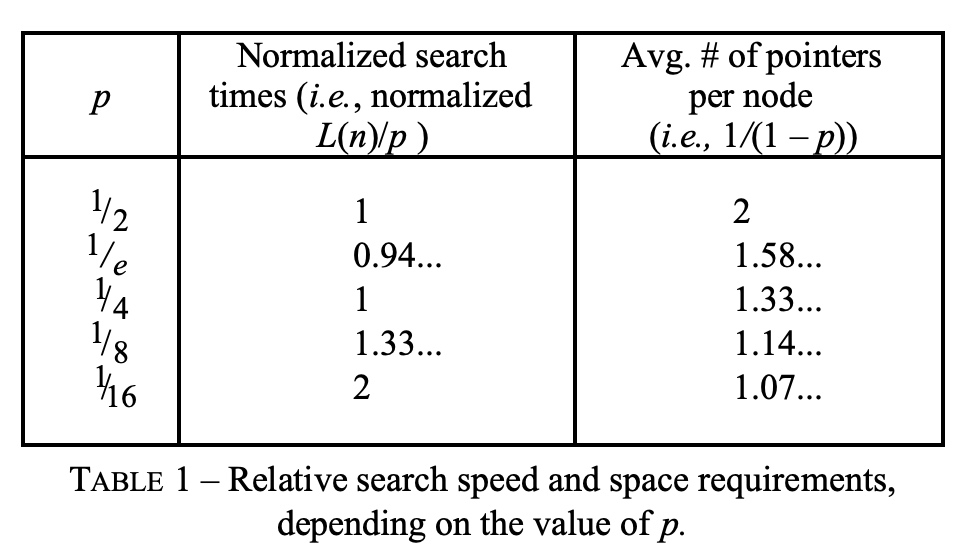
但是，一般经验对于 prob 存在 magic number, 比如skiplist中实现的，

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
func (list *SkipList) randLevel() int {
	if list.maxLevel <= 1 {
		return 1
	}

	// Use log_2(list.length) * 4 as estimated max level.
	estimated := bits.Len(uint(list.length)) * 4

	if estimated > list.maxLevel {
		estimated = list.maxLevel
	}

	// prob should be a bit more than 1/2 chance to make level balanced.
	// This value is selected by some random Get tests on a random generated list.
	// The magic number 3/8 works best when list size < 10,000,000.
	const prob = math.MaxInt32 * 3 / 8

	for i := 1; i < estimated; i++ {
		if list.rand.Int31() < prob {
			return i
		}
	}

	return list.maxLevel - 1
}

还有个skiplist-survey分析了，go实现的不同skiplist性能。

概率

关于skiplist的核心：概率问题，参考A Skip List Cookbook

理想情况下，我们希望从下往上不同的level层，元素逐级减少，像B树一样，完美地二分了数据。但在skiplist中，做到这一点的是概率函数，就如上面说的maxLevel和p。

重新理解概率因子 p：1/p的元素，它们在 level i层，同时也会在 level i+1 层。也就是说，假设 level 0 层有10个元素，p=1/2，我们希望 level 1 层有5个元素，level 2 层有 2个元素

概括来说：在level L层，期望有 1/p 个元素。这样一层一层叠到顶层，就是1/p * 1/p * 1/p = 顶层元素出现的概率。我们希望，skiplist可以按照这种方式组织起来，所以对一个元素，计算level时候，它的概率，是随着 level 层数增加，相应变低的。这就可以理解，上面代码里的for循环目的：for i := 1; i < estimated; i++，为了多次求概率，如果越往上层走，在for里满足if的几率就越低，就可以满足最初的expectation。

根据，Cookbook里的描述，当p=1/2时，选择maxLevel=32可以满足32bit的数据。

不过 skiplist 非常依赖于随机数的均衡性，当前这方面其实没有做特殊优化，如果要做的更好的话理论上应该根据 key 的值和分布情况来确定 rand 算法才行。

最后，问题：skiplist 不像 B-Tree 对内存缓存友好，因为跳表的节点很小，而且在内存中是随机分配的。Unrolled lists来对这种情况就行了改进，本质是link pointer从指向一个item到指向一块item，里面包含了多个elements。很大的提高了cache性能。

无序LSM存储

之前的数据结构，B树/FD树/SSTable都是按照key顺序存储的。无序存储，允许我们按照插入顺序存储记录，减少写入的开销。

Bitcask

Bitcask 它是一个无序的日志存储引擎，没有使用memtable进行缓冲，而是将数据直接存储在日志文件中的。

为了检索key，它使用keydir，类似内存中HashTable，用来保存 key与最新数据 的地址指针。它会在启动期间，从日志中重建。如下图

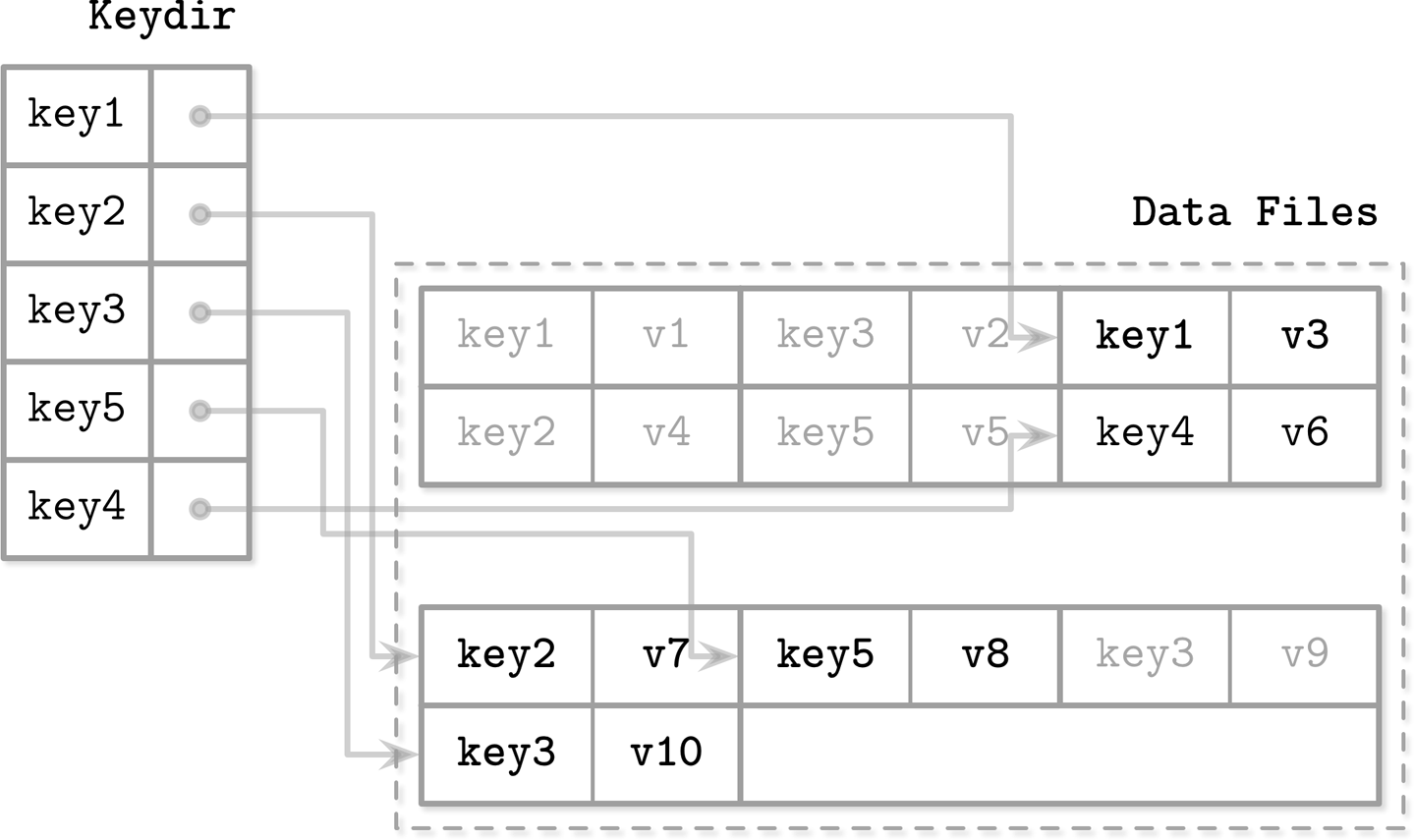
keydir的key始终指向的最新数据的指针。而旧数据，会在compaction阶段丢弃掉。

pros: 数据直接记录在日志文件中，不需要单位维护一个WAL，减少了写放大和空间放大。

cons: 只支持单点查询，不允许范围扫描，并且在启动时候，需要足够大的内存去Hold keydir

golang bitcask

WiscKey

range scan对RDBMS还是很重要的，有没有一种数据结构支持无序存储和 range scan呢？

WiscKey: Separating Keys from Values in SSD-conscious Storage

通过在LSM树中，保存sorted keys，并将数据存储在unordered applend-only的文件中(vLogs: value logs)，来降低写放大问题。如下图，核心是：只将key存储在LSM-Tree中，value单独存储

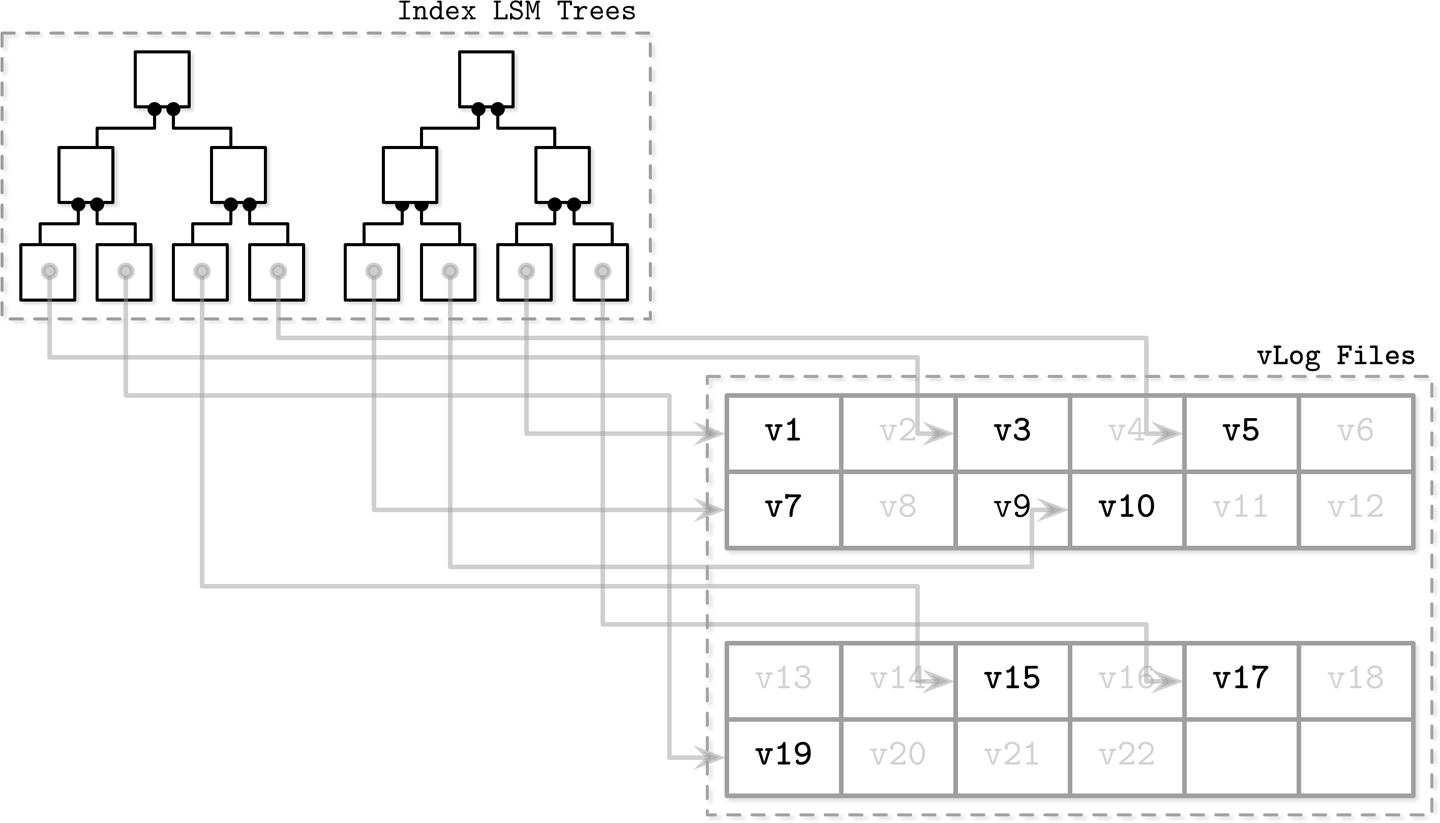
Key存储在LSM-Tree中，还是如上面介绍的那样，包含 WAL -> memtable -> SSTable 这个流程。

因为value从LSM-Tree中拆分出去后，只保留了key，所以在compaction节点数据量就会小很多，带来更好的写性能。

cons: 参考papers里的challenges

由于vLogs是未经排序的，在range scan时候，需要大量随机I/O
由于Key-Value是分开存储，LSM-Tree compaction只会GC掉invalid的key，对于values需要单独的机制GC(回查LSM+移动vLogs 方式解决)

论文中提到，解决随机I/O的方式是通过 SSD parallel I/O 特点来perfetch vLogs。

rocksdb

针对上面LSM-Tree的各种概念，我们可以映射到rocksdb wiki中，便于理解