Used Algorithms
首先,摘抄下怎么记忆算法里观点:
初中学习几何证明的时候,你会不会傻到去背一个定理的证明?不会。你只会背结论。 为什么?一方面,因为证明过程包含大量的细节。另一方面,证明的过程环环相扣,往往只需要注意其中关键的一两步, 便能够自行推导出来。算法逻辑描述就好比定理,算法的证明的过程就好比定理的证明过程。 但不幸的是,与数学里面大量简洁的基本结论不同,算法这个“结论”可不是那么好背的,许多时候, 算法本身的逻辑就几乎包含了与其证明过程等同的信息量,甚至算法逻辑本身就是证明过程(随便翻开一本经典的算法书,看几个经典的教科书算法,你会发现算法逻辑和算法证明的联系有多紧密)。 于是我们又回到刚才那个问题:你会去背数学证明么?既然没人会傻到去背整个证明,又为什么要生硬地去背算法呢?
不背,就要去理解算法本质。如分治算法、贪心算法、动态规划等。再从它们衍生出来具体的算法。
我习惯先将基础步骤,用纸笔写出来过下流程。然后根据写出来的流程,写代码逻辑。
贪心算法
Dijkstra
使用了BFS解决 非负权有向图的单源最短路径问题。本质是贪心算法:局部最优解结合成的全局解一定是全局最优解。
图的存储有两种:矩阵和邻接表。对于稀疏图(E边数 远小于 V*V 顶底数 )来说,邻接表的效率高于矩阵。
我们先采用矩阵来存储,邻接表算法类似。原理是广度优先搜索。然后通过 松弛操作,比较出路径的最短距离。
BFS:从一个顶点V0开始,辐射状地优先遍历其周围较广的区域。类似这里的松弛操作。
先构造矩阵:
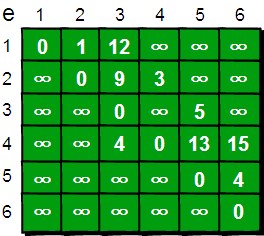
该图要横着看,如第一行表示1节点 距离 其他节点的距离。∞表示1节点到4不通。
求1号到其他点的最短路径 具体操作:
- 先构造一个dis数组表示1号点距离其它点的最短路径。
- 从dis数组里找到距离1号最近的一个点2号,然后将2号的所有 出边(2->3, 2->4) 进行松弛操作。即dis[3] 和 dis[2]+e[2][3]比较出最小值,再更新dis数组。dis[4] 和 dis[2]+e[2][4]比较更新。对所有出边松弛完后,记录2号点已经找到。即已经找到dis[2]的最短路径。
- 从dis数组里3/4/5/6元素中 找距离1号最近的点,重复上一步的类似操作。
- 待所有点都已经标记成找到最小路径后,结束。
思路相同点:从剩余点中 找出距源点最近的点A,再对A点出边松弛操作,记录最小路径至dis。从剩余点中移除A。
参考: Dijkstra
动态规划
把问题 分解成相对简单的 子问题,然后求解。
01背包问题
问题: 给定一组多个(n)物品,每种物品都有自己的重量(w)和价值(v),在限定的总重量/总容量(C)内,选择其中若干个(也即每种物品可以选0个或1个),设计选择方案使得物品的总价值最高。
本质是动态规划:每次决策依赖于上一次的求解,形成决策序列 产生最优结果。
原理:通过分治 拆分成相互联系的子问题,当前决策依赖于上一次的最优决策,依次求解。
算法思路:分解成子问题解决。
1、定义状态:dp[i][c]表示前i件物品恰放入一个容量为c的背包可以获得的最大价值。
2、dp[i][c]值有两种情况:
c < weight[i]: 背包已经放不下了:当前背包的最大容量c < 该物品的重量weight[i]。这时候取dp[i-1][c]。
c >= weight[i]: 背包还可以接着放。分以下两种:
不放 第i件物品,dp[i][c] = dp[i-1][c]。即背包容量不变 求上一次(i-1)的最优求解。
放 第i件物品,dp[i][c] = dp[i-1][c-weight[i]] + value[i]。即背包容量减少 求上一次(i-1)容量为 c-weight[i] 的最优求解 + 第i个物品的最大价值。
描述为的状态转移方程是:
| |
所以,注意转移方程 产生的决策序列。每次依赖上一次最优求解。 转移方程出来后,构造矩阵写算法就很容易了。
3、构造状态矩阵:
该矩阵中的每个值的求解都代表一个更小的背包问题。 构造完矩阵后,取dp[maxI][maxC],即获得最大价值。
这里不论按照行去构造矩阵,还是按照列去构造矩阵。都可以构造出最后的结果。
4、构造矩阵求最大价值:
5个元素,它们对应的value和weight在代码中,构造的矩阵如:
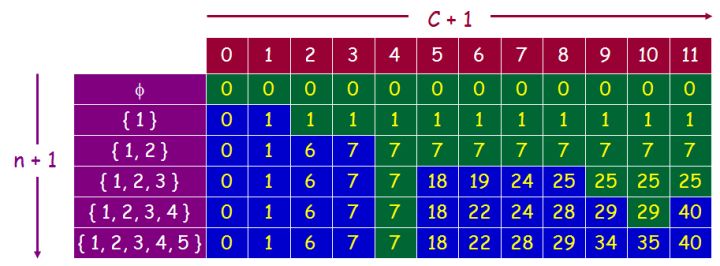
5、求最大价值时选择的方案
注意:我们需要找的是 元素的组合,而不是顺序。所以,我们只需关注 在构造矩阵时 选择第i件物品的条件。然后从后往前推即可。
从上面代码看出,发生取第i件物品的条件:
dp[i][c] == dp[i-1][c-w] + v ,相对于 dp[i][c] = max(dp[i-1][c], dp[i-1][c-w]+v) 而言,条件也可以看做 dp[i][c] != dp[i-1][c] 。
表现在图上,从表格右下角“往回看”如果是“垂直下降”就是发生了 dp[i][c] == dp[i-1][c] ,而只有“走斜线”才是“取了”物品。
具体理解也可以是:
- 前5个元素容量11最大40,前4个元素容量11最大40,所以没有用到第5个元素。
- 前3个元素容量11最大25,前4个元素容量11最大40,所以肯定用到了第4个元素。表现在矩阵上就是dp[3][11] != dp[4][11],然后总容量11 减去 第4个元素的容量 6 等于5。
- 然后在容量为5,前3个元素组合的列找。前3个元素容量5最大18,前2个元素容量5最大7,所以肯定用到了第3个元素。然后总容量5 减去 第3个元素的容量 5 等于0。到此容量用完退出遍历,即找到了最大价值组合。
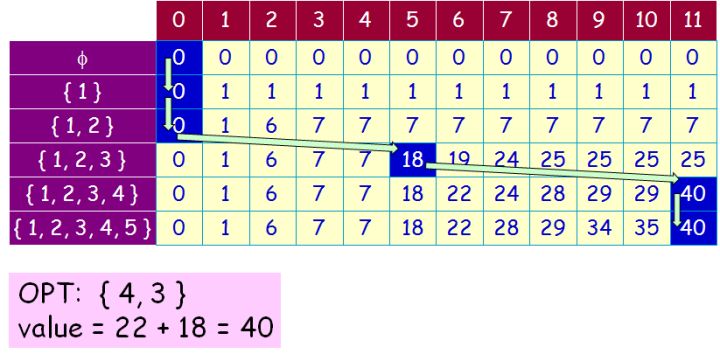
对于小数背包问题,可以先将小数化成单位更小的整数,在利用dp矩阵处理。
参考:01背包问题
Graph Theory
Tarjan寻找有向图的强连通分量
具体场景:分析有向图是否有环,即是否存在强连通分量(len>1)
- 强连通:在有向图G中,如果两个vertex间有路径,则称该两点是强连通的。strongly connected
- 强连通图:在有向图G中,任意两个vertex都是强连通的。
- 强连通分量:在有向图G中,存在的极大连通子图,称为强连通分量。strongly connected components - SCC
Tarjan算法:对图DFS,深度优先搜索时,每个SCC都是搜索树中的一颗子树。
先看视频:
关键概念:
Low-Link Values: 一个节点 可到达的 最小id的 节点,including ifself
用语言描述步骤就是:
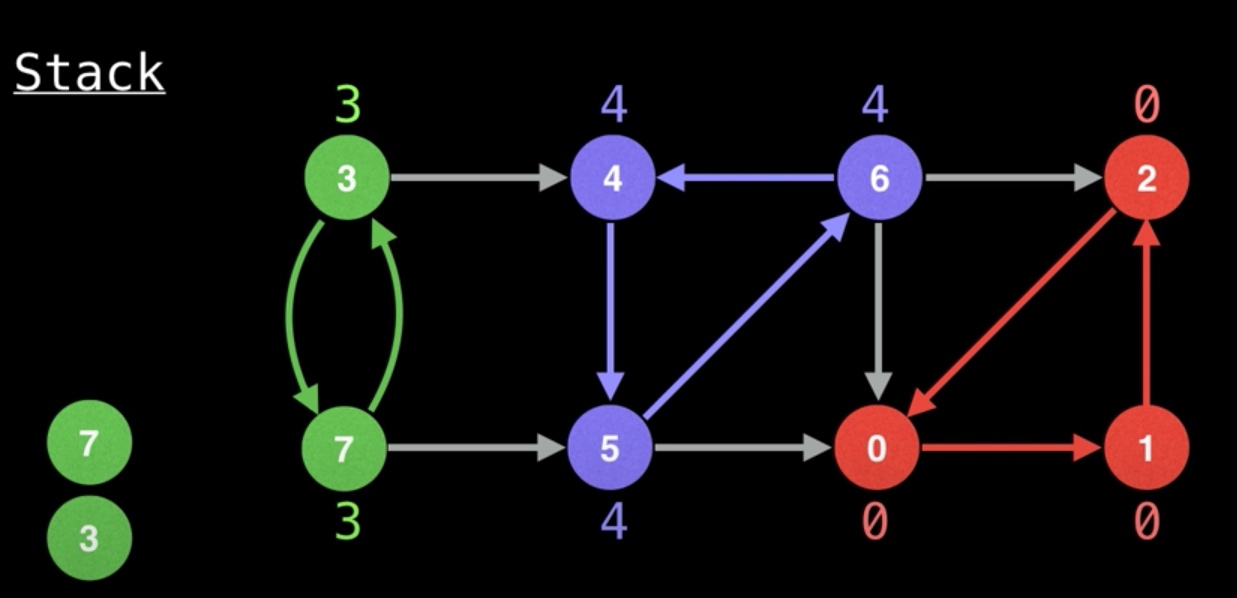
第一步:随机顶点,DFS,构造DFN(节点访问到的序号) 与 Low(初始化为dfn)。
如下图中,DFN就是节点访问到的序号,圆圈下的白数字 是 Low-Link Value,即初始化为DFN。
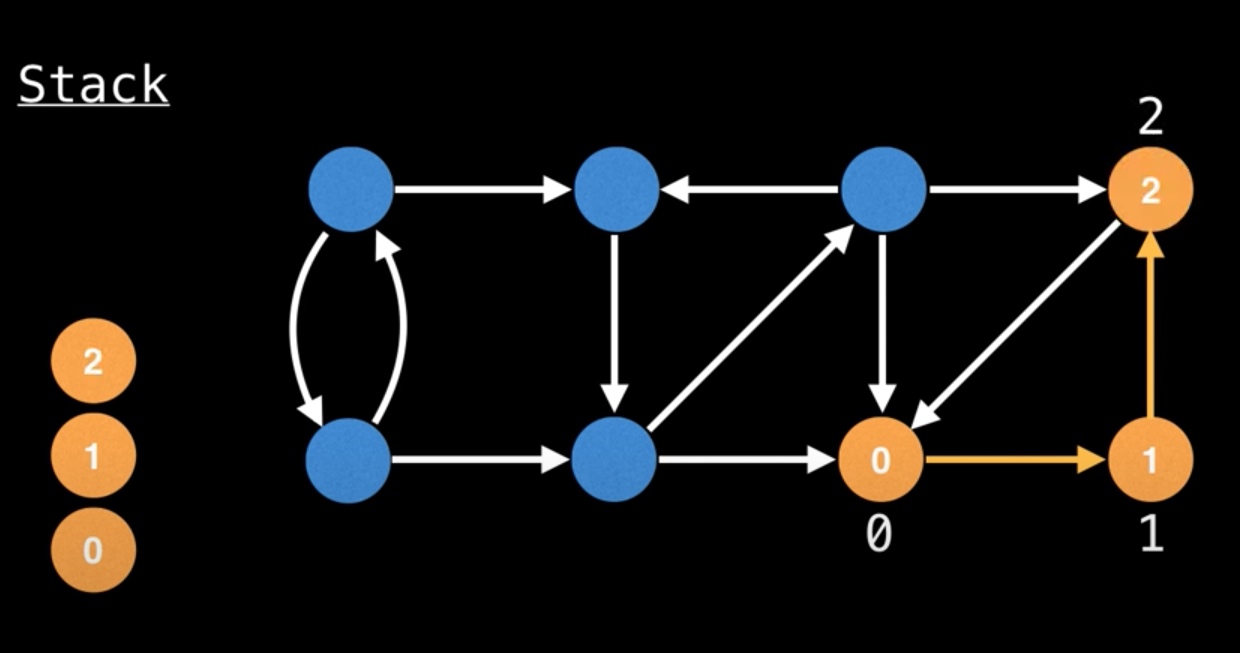
第二步:在DFS时候,一个顶点的邻居如果在stack中,则它的lowlink = min(自己的lowlink, 邻居的lowlink)
如lowlink[2] = min(lowlink[2], lowlink[0]) = 0
进而dfs回退时继续计算:
lowlink[1] = min(lowlink[1], lowlink[2]) = 0
lowlink[0] = min(lowlink[0], lowlink[1]) = 0
最终,dfs回退到节点序号0时候,lowlink[0] = dfn[0]。此时,pop出stack中的所有节点,即为一个SCC。
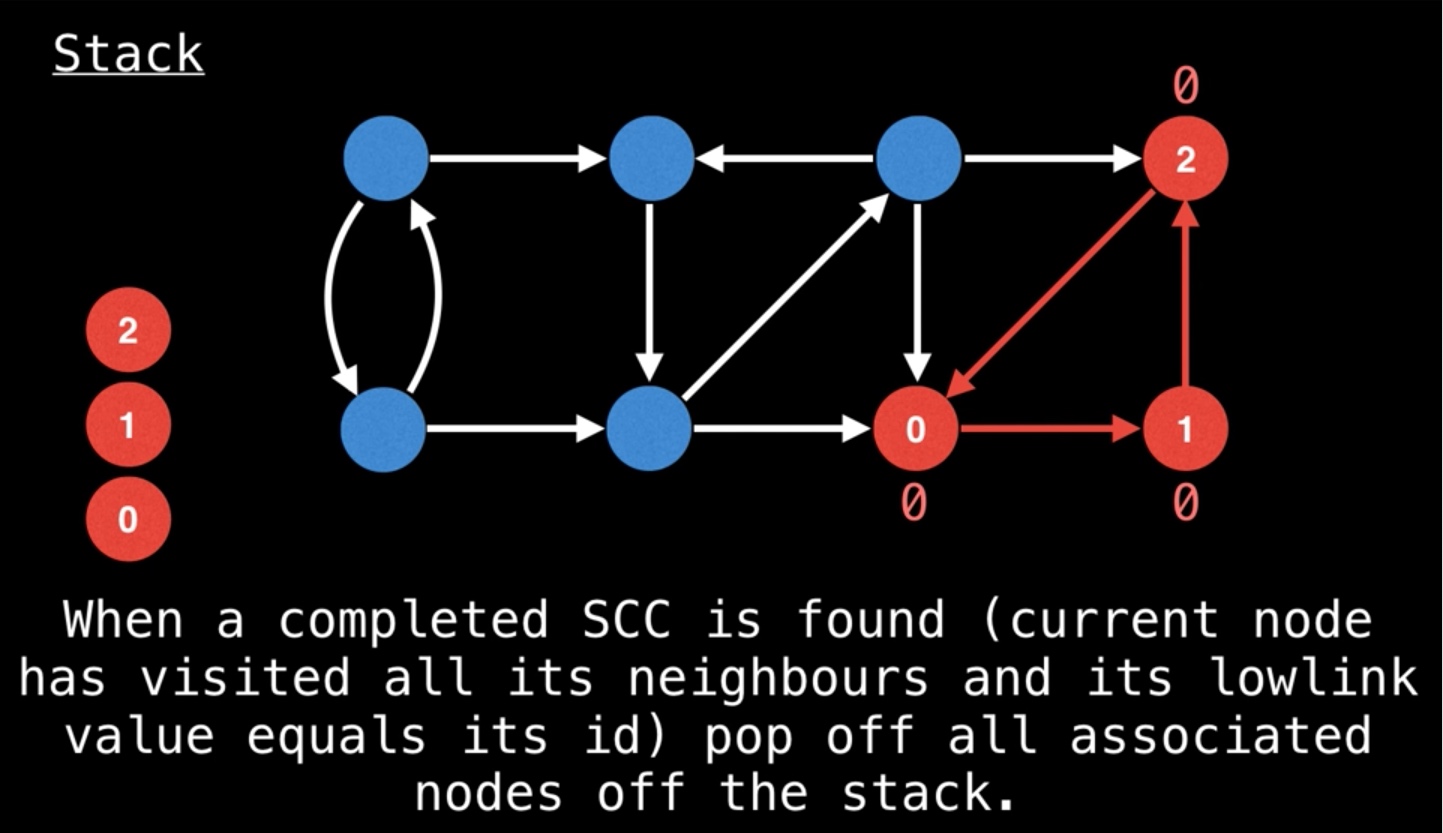
第三步:和第二步类似,dfs其它节点。注意,遍历到不在stack上的节点,忽略它的lowlink。
最终所以SCC如下图